Plinko Simulation
ProjectFor my final project for ME314: Machine Dynamics, I simulated the game plinko from scratch. A plinko chip (represented as a square) falls under gravity through a series of plinko pegs (also represented by squares). The chip experiences elastic collisions with the pegs as it falls, and is subject to friction as it moves across the board.
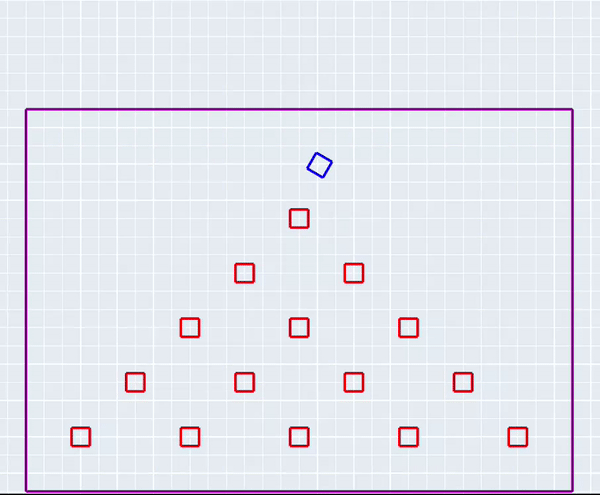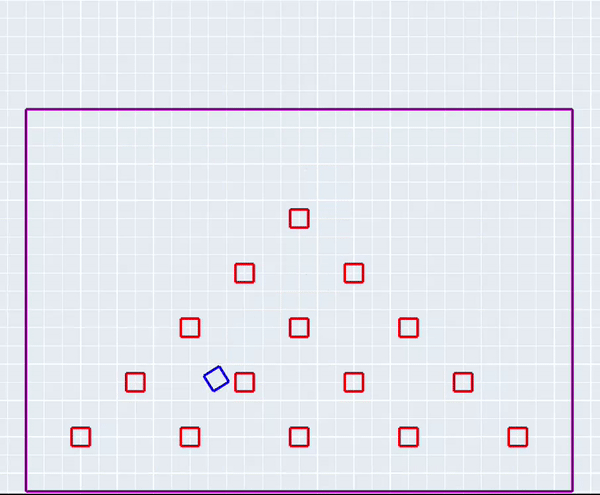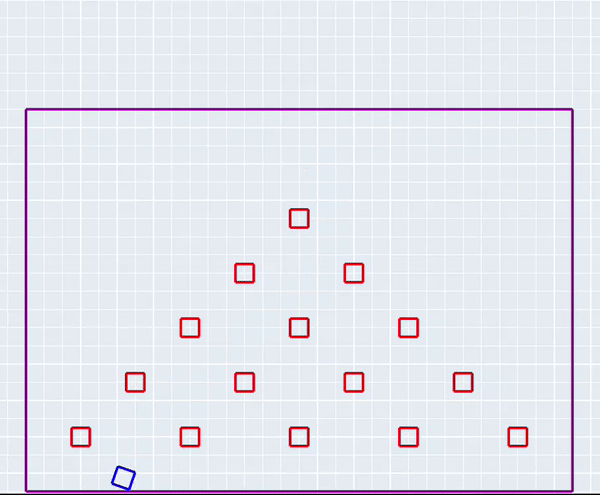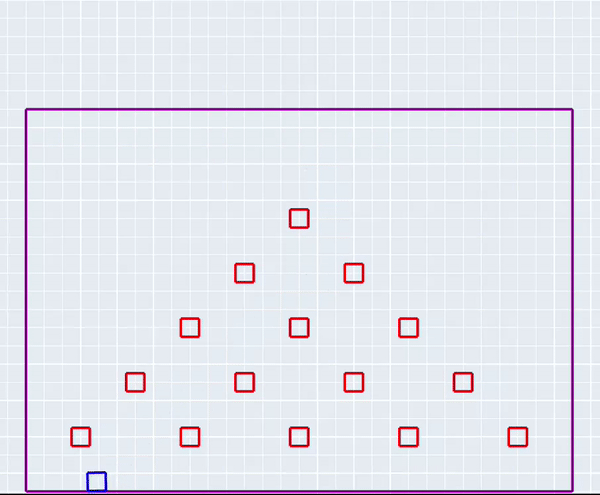
The simulation in action!
Euler Lagrange Equations
To simulate this system, I kept track of 3 state variables representing the position and orientation of the plinko chip: x, y, and theta. I then generated and solved the Euler Lagrange equations using SymPy to get descriptions of the motion. These equations incorporated the rotational energy of the chip as it spun as well as the forces of friction and gravity.
Collisions
What made this project complicated was simulating the huge number of possible collisions, and calculating the respective impact update equations. These update the velocities of each of my state variables (x, y, and theta) during the collision using the fact that the Hamiltonian of the system stays conserved, as well as that the change in momentum is perpendicular to the contact surface.
As a baseline, I had 16 impact conditions that corresponded to each corner of the chip hitting the 4 bounding walls of the plinko board. For each peg that I added to the system, I needed to add 32 impact conditions and 32 corresponding impact update equations. These correspond to each of the 4 corners of the peg colliding with each of the 4 sides of the chip (16), plus each of the 4 corners of the chip colliding with each of the 4 sides of the peg (another 16). After testing my code extensively with only one peg, I abstracted peg creation into a loop so I could add as many as I liked. My final simulation contained 5 rows of pegs, which corresponds to 496 possible impacts!